1.Hypothèses et définitions

Imaginons un univers dont la masse augmente constamment. Ce surplus de masse provoque une augmentation de volume de l’espace qui pousse donc les corps vers l’extérieur. Ce phénomène expliquerait, entre autres, l’expansion de l’univers. Il me paraît, en cohérence avec le sens que je donne aux constantes, de prendre comme débit massique de l’univers le rapport entre la masse et le temps de Planck.
L’expansion de la masse de l’univers découle naturellement de la notion d’espace propre, exposée précédemment, qui associe un volume d’espace à une masse. En effet, si l’espace de l’univers est en expansion alors l’espace propre de l’univers l’est aussi. Ce qui implique nécessairement que la masse associée doit l’être aussi.

On suppose aussi que l’univers est une boule de rayon R_U.

2.Calcul des grandeurs de l’univers

Soit m_p la masse de Planck et t_p le temps de Planck. Je détermine un débit massique d_mp de Planck que je suppose constant dans le temps :
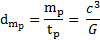
Le calcul numérique nous donne : d_mp = 4,037256.10³⁵ kg.s^-1

Le débit massique nous permet de calculer la masse de l’univers.
Soit M_U la masse de l’univers à un instant t. Soit H_U la constante d’Hubble à notre époque et T_U la période durant laquelle l’univers est en expansion à un instant t. On suppose que T_U=1/H_U . Je prends comme valeur H_U = 2,380x10^-18 s^-1.
La masse de l’univers s’exprime comme suit :
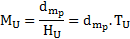
M_U = 4,037256.10³⁵ / (2,380.10^-18)
M_U = 1,696.10⁵³ kg

La tension de l’espace ne s’applique pas directement au corps, cependant elle s’applique à l’espace lui-même. Par conséquent, la masse de l’univers crée une tension de l’espace qui agit sur la surface de l’extrémité de l’univers. Si on applique la loi de Newton au système isolé qui est l’univers, alors on obtient : M_U.a_U = F_U
F_Uest la tension qui s’applique à la surface de l’univers et
a_U est l’accélération de l’expansion de l’espace et non l’accélération de la masse de l’univers

Soit ρ_U la masse volumique de l’univers et R_U le rayon de l’univers.
On obtient donc :

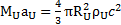
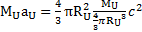
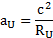
De plus, nous pouvons montrer, à l’aide de la loi d’Hubble, que l’expansion de l’univers suit l’expression suivante :
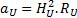
Nous obtenons donc 2 expressions de l’accélération de l’expansion de l’univers. L’une que j’ai obtenue avec la tension spatiale et l‘autre que j’ai établie via une réflexion sur l’expansion de l‘univers : 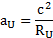et
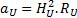
Celles-ci permettent d’exprimer la relation suivante :
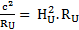
c² = H_U².R_U2
c = H_U.R_U ou c = - H_U.R_U. Je vais, dans cette étude, considérer que c est positive. J'obtiens une relation qui a la même forme que la loi d’Hubble suivante : c=H_U.R_U
On remarque que la vitesse d’expansion de l’univers est égale à la vitesse de la lumière dans le vide

Cette relation nous permet donc de calculer le rayon de l’univers :

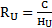
R_U = 2,997925.10⁸ / (2,380.10^-18)
R_U = 1,26.10²⁶ m

On considère que la masse de l’univers se trouve contenue dans un volume sphérique de rayon R_U. Exprimons la masse volumique de l’univers :


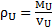
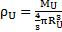
ρ_U = 1,696.10⁵³ /[4/3π(1,260.10²⁶)³]
ρ_U = 2,026.10^-26 kg.m^-3

Exprimons maintenant la variable d’Hubble H_U. Nous avons précédemment montré que :
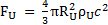et 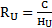, donc


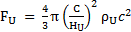
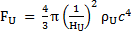
Nous avons aussi montré dans la partie « 3. Equivalence force de Planck / tension spatiale de l’univers » que 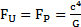, donc :

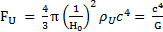
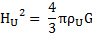
3.Equivalence force de Planck / tension spatiale de l’univers

Nous savons que :
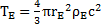
Je vais appliquer cette relation à l’ensemble de l’univers de rayon Ru. Je suppose que l’univers est homogène, donc la masse volumique de l’univers ρ_U est constante à l’échelle de l’univers.

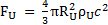
F_U = 4/3.π.(1,26.10²⁶)².2,026.10^-26.(2,997925.10⁸)²
F_U = 1,21.10⁴⁴ N
F_U est la tension en un point de la surface à l’extrémité de l’univers.

Je calcule maintenant la force de Planck

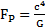
F_P = (2,9979246.10⁸)⁴/(6,674.10^-11)
F_P = 1,21.10⁴⁴ N

On remarque que la tension superficielle spatiale correspond exactement à la force de Planck F_P. Nous allons démontrer cette égalité ci-dessous :

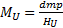
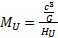or,
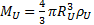
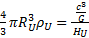En multipliant cette expression par 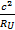à droite et à gauche, nous obtenons l’expression suivante :

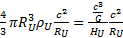
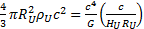. Or nous avons démontré que 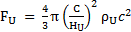et
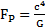
Donc 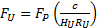, de plus on a aussi démontré précédemment que c=R_U.H_U

Par conséquent, j’en conclus que : F_U=F_P

4.Expression des constantes G et c

Selon le principe des constantes universelles, toutes les constantes cosmologiques universelles sont définies par les grandeurs qui caractérisent l’univers, à savoir :
M_U : masse de l’univers
R_U : rayon de l’univers
T_U : période d’expansion de l’univers

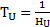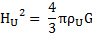On a posé .Or, et
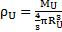
Donc
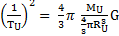
La constante gravitationnelle s'exprime sous la forme suivante :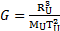

Nous avons aussi exprimé précédemment que c = R_U.H_U, la vitesse de la lumière dans le vide s'exprime comme suit :

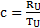
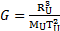et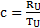 nous donnent la relation suivante:

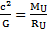
Auteur : Khalid Jerrari

---